Математика - это язык, на котором написана книга природы.
РЕШЕНИЕ ЗАДАЧ, КОНТРОЛЬНЫХ РАБОТ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Галилео Галилей

Главная

Оплата

Примеры

Учебники

Поток и циркуляция векторного поля

Условие:

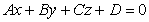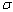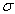Даны векторное поле F = Xi + Yj + Zk и плоскость (р) , которая совместно с координатными плоскостями образует пирамиду V. Обозначим основание пирамиды, принадлежащее плоскости (р), через , ограничивающий контур - через , нормаль к 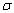, направленную вне пирамиды V , - через n. Требуется:

1) вычислить поток векторного поля F через поверхность 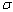в направлении нормали n;

2) вычислить циркуляцию векторного поля F по замкнутому контуру 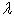непосредственно и применив теорему Стокса к контуру 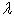и ограниченной им поверхности 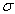с нормалью n;

3) вычислить поток векторного поля F через полную поверхность пирамиды V в направлении внешней нормали к её поверхности непосредственно и применив теорему Остроградского. Сделать чертёж.

F = (x + z)i; (p) x + y + z – 2 = 0.

Решение:

1) Поток П векторного поля F через поверхность σ равен поверхностному интегралу

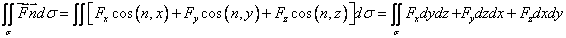П =

{выразим x из уравнения плоскости и перейдем от поверхностного интеграла к двойному} =

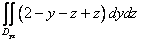
{- проекция поверхности σ на плоскость уОz }=

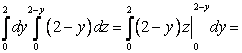
2) Циркуляция Ц векторного поля F по контуру λ равна линейному интегралу

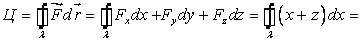
На АВ: у = 0; x + z = 2. На ВС: x = 0, dx = 0. На СА: z = 0.

Ц = .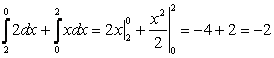

Найдем циркуляцию по формуле Стокса.

Ц = = .

Обход контура λ в правой системе координат должен проводиться против часовой стрелки, если смотреть в направлении вектора (на рисунке направление указано стрелками).