Главная
Оплата
Примеры
Учебники
|
|
Отношения и их свойства
Условия:
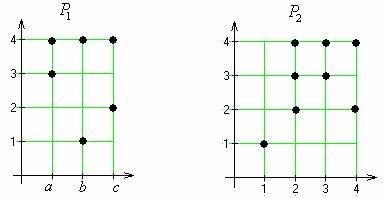
Даны два конечных множества: А={a,b,c}, B={1,2,3,4};
бинарные отношения P1
Í A´
B, P2
Í B2.
Изобразить P1, P2 графически. Найти P = (P2◦P1)–1.
Выписать области определения и области значений всех трех
отношений: P1, P2, Р. Построить матрицу [P2],
проверить с ее помощью, является ли отношение P2
рефлексивным, симметричным, антисимметричным, транзитивным. P1 = {(b,1),(b,4),(a,3),(a,4),(c,4),(c,2)};
P2 = {(1,1),(2,4),(2,3),(2,2),(3,3),(3,4),(4,2),(4,4)}.
Решение:
Произведением
 отношений
 и
 называется
отношение
 .
Запишем
 в
виде пар.
 .
 .
 .
 .
 .
 .
 .
 .
 .
 .
 .
 .
Убрав одинаковые пары, получим
 .
Обратное отношение
 .
Областью определения
отношения
 называется
множество
 .
Областью значений
называется множество:
 .
 .
 .
 .
 .
 .
 .
Матрица отношения
 :
 .
Бинарное отношение
 на
 называется
рефлексивным, если
 .
На главной диагонали матрицы такого отношения
стоят единицы.
Отношение
рефлексивно.
Отношение называется симметричным, если
 ,
т. е.
 или
 .
Матрица симметричного отношения симметрична.
Отношение
не
симметрично.
Отношение называется антисимметричным,
если
 ,
т. е. в матрице
вне главной
диагонали все элементы равны нулю.
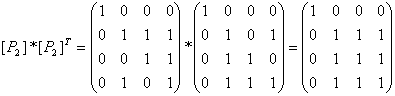
Отношение
не
является антисимметричным.
Отношение называется транзитивным, если
 ,
т. е.
 .
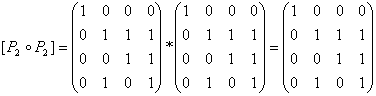
Отношение
транзитивно.
|
|
